Step1: Structure of an optimal parenthesization: Our first step in the dynamic paradigm is to find the optimal substructure and then use it to construct an optimal solution to the problem from an optimal solution to subproblems. It can also be noticed that there exists only O (n 2 ) different sequence of matrices, in this way do not reach the exponential growth. But that it can be observed that checking all possibilities will lead to an exponential number of total possibilities. One possible answer to the first question for finding the best value of 'k' is to check all possible choices of 'k' and consider the best among them. How to parenthesize the subsequence A 1.k andA k+1.n?.It can be seen that the dimension of A i,j is p i-1 x p j matrix.ĭynamic Programming solution involves breaking up the problems into subproblems whose solution can be combined to solve the global problem.Īt the greatest level of parenthesization, we multiply two matrices
Let A i,j be the result of multiplying matrices i through j. Construct the optimal solution from the computed information.
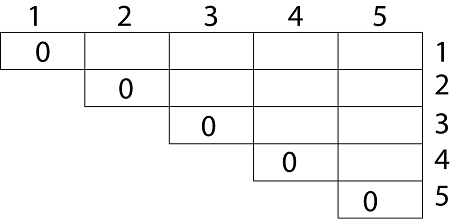Compute the value of an optimal solution in a bottom-up fashion. Define the value of an optimal solution recursively. Characterize the structure of an optimal solution. Which shows that 4 n grows faster, as it is an exponential function, then n 1.5.ĭevelopment of Dynamic Programming Algorithm Now there are 'L' ways of parenthesizing the left sublist and 'R' ways of parenthesizing the right sublist then the Total will be L.R:Īlso p (n) = c (n-1) where c (n) is the nth Catalon number It can be observed that after splitting the kth matrices, we are left with two parenthesized sequence of matrices: one consist 'k' matrices and another consist 'n-k' matrices. No of Scalar multiplication in Case 1 will be: (A 1,A 2),A 3: First multiplying(A 1 and A 2) then multiplying and resultant withA 3. A 1,(A 2,A 3): First multiplying(A 2 and A 3) then multiplying and resultant withA 1. Three Matrices can be multiplied in two ways: It is also noticed that we can save the number of operations by reordering the parenthesis.Įxample1: Let us have 3 matrices, A 1,A 2,A 3 of order (10 x 100), (100 x 5) and (5 x 50) respectively. It can be observed that the total entries in matrix 'C' is 'pr' as the matrix is of dimension p x r Also each entry takes O (q) times to compute, thus the total time to compute all possible entries for the matrix 'C' which is a multiplication of 'A' and 'B' is proportional to the product of the dimension p q r.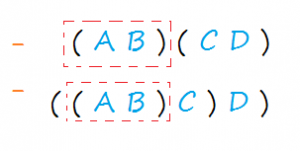 
By this, we mean that we have to follow the above matrix order for multiplication but we are free to parenthesize the above multiplication depending upon our need. Matrix Multiplication operation is associative in nature rather commutative.
0 kommentar(er)
